Break-even Quantity shows the level of output that the business must produce and sell at which Sales Revenue equals Total Costs (TC). At Break-even Quantity neither a profit nor a loss is made.
In order to calculate and find out Break-even Quantity, Break-even Analysis shall be undertaken. Break-even Quantity can be determined either by using the Equation Methods or the Graphical Method:
1. The Equation Methods. There are two ways to calculate and determine Break-even Quantity using two different formulae:
a.) The Equation Method 1: Sales Revenue = Total Costs (TC)
b.) The Equation Method 2: Break-even Quantity (BEQ)
2. The Graphical Method. By constructing the Break-even Chart.
The Graphical Method
The Break-even Chart should be constructed to find out Break-even Quantity using the Graphical Method.
The purpose of constructing the Break-even Chart is to show the relationship between the business’s Sales Revenue and various costs at different levels of Output. The Break-even Chart, when properly and clearly constructed, can be used to work out the level of Output that the business must produce and sell to earn Sales Revenue.
Because that Sales Revenue will exactly equal Total Costs (TC) of producing that level of Output, that particular Output will be Break-even Output.
How to construct a simple Break-even Chart?
The Break-even Chart requires two axes. The horizontal x-axis for the number of products produced and sold, and the vertical y-axis for Sales Revenue and Total Costs (TC). Both axes start from 0. The x-axis is labelled as ‘Output (in units)’ and the y-axis is labelled as ‘Costs and Revenues (in USD$)’.
The Break-even Chart itself shows four pieces of information:
- Sales Revenue. It is calculated by multiplying selling Price by Output.
- Fixed Costs (FC). In the short term, they will not vary with the level of Output. These must be paid whether the firm produces any products or not.
- Variable Costs (VC). In the short term, they will vary with the level of Output. If the firm does not produce anything, these costs do not need to be paid. We will assume, initially at least, that Variable Costs (VC) vary in direct proportion to Output.
- Total Costs (TC). Which is the addition of Fixed Costs (FC) and Variable Costs (VC).
Let’s take a closer look at a typical Break-even Chart:
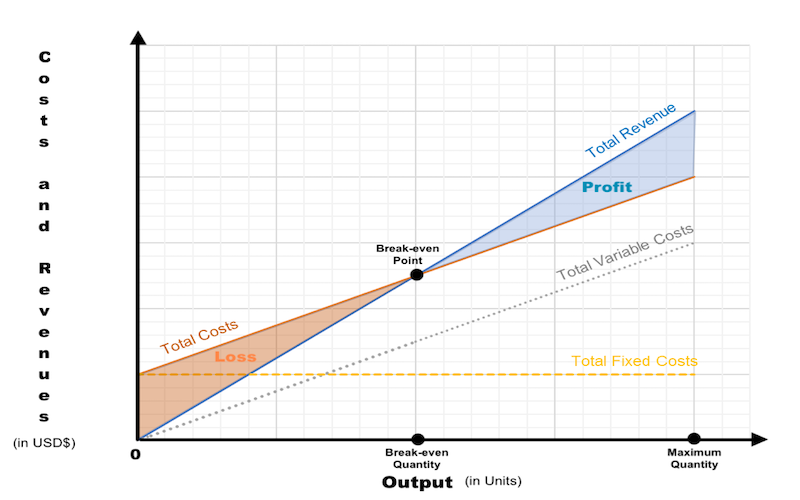
To construct the Break-even Chart, we need to plot the curves that indicate Sales Revenue and Total Costs (TC). The Sales Revenue and Total Costs (TC) information at the 0-Output level and at maximum Output level is used to produce the Break-even Chart. Therefore, a business needs to know its:
- Sales Revenue. Sales Revenue at 0 Output and at maximum Output. Sales Revenue always starts at the origin 0 because, if no sales are made, there cannot be any Sales Revenue.
- Fixed Costs (FC). Fixed Costs (FC) at 0 Output. Fixed Costs (FC) are the same at 0 Output and the same at maximum Output. The fixed-cost line is horizontal, showing that Fixed Costs (FC) are constant at all Output levels. This is because we assume that Fixed Costs (FC) are the same and will not change within one year.
- Variable Costs (VC). Variable Costs (VC) at 0 Output and at maximum Output. The variable-cost line starts from the origin 0, because if no goods are produced, there will be no Variable Costs (VC). They are not really necessary, but the curve is drawn anyway to help with understanding how the chart is constructed. Variable Costs (VC) increase as Output continues to increase. Variable Costs (VC) at maximum Output are calculated as the Average Variable Cost (AVC) multiplied by maximum Output.
- Total Costs (TC). Total Costs (TC) at 0 Output and at maximum Output. The total-cost line begins at the level of Fixed Costs (FC). Fixed Costs (FC) plus Variable Costs (VC) give Total Costs (TC) at any given Output.
The point at which the total-cost line and sales-revenue line cross each other is Break-even Point. Break-even Point indicates the costs and revenues at Break-even Quantity.
At production and sales levels below Break-even Point, the business is making a loss. While at production and sales levels above Break-even Point, the business is making a profit.
Let’s take a look at a real-life example.
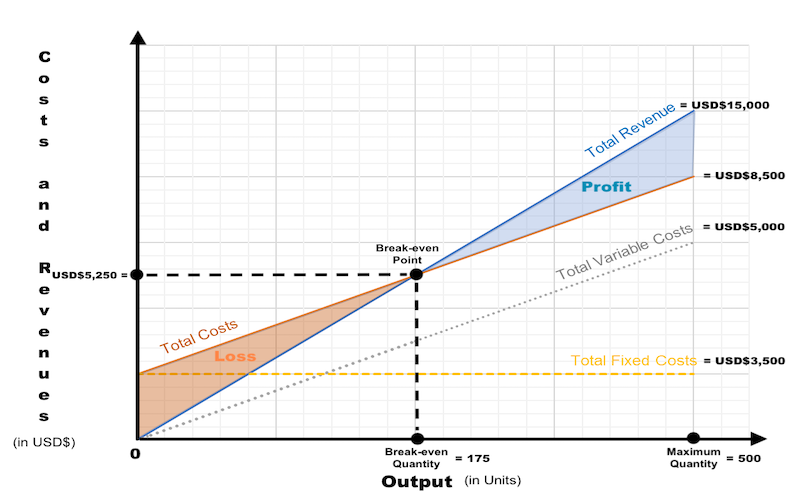
Example for the Graphical Method 2 A hamburger restaurant has Fixed Costs (FC) of USD$3,500 per month. Variable Costs (VC) are USD$10 per hamburger, and the selling price of one chicken hamburger is USD$30. The maximum number of hamburgers the restaurant can produce per month is 500. Question: How many chicken hamburgers does this retailer must sell per month in order to break-even? Fixed Costs (FC) = USD$3,500 Average Variable Cost (AVC) = USD$10 Maximum Quantity = 500 chicken hamburgers Let’s calculate Sales Revenue at Maximum Quantity: Sales Revenue at Maximum Quantity = Price x Maximum Quantity Sales Revenue at Maximum Quantity = USD$30 x 500 Sales Revenue at Maximum Quantity = USD$15,000 Let’s calculate Total Costs (TC) at Maximum Quantity: Fixed Costs (FC) at Maximum Quantity= USD$3,500 Total Variable Costs (TVC) at Maximum Quantity = Average Variable Cost (AVC) x Maximum Quantity Total Variable Costs (TVC) at Maximum Quantity = USD$10 x 500 Total Variable Costs (TVC) at Maximum Quantity = USD$5,000 Total Costs (TC) at Maximum Quantity = Fixed Costs (FC) + Total Variable Costs (TVC) at Maximum Quantity Total Costs (TC) at Maximum Quantity = USD$3,500 + USD$5,000 Total Costs (TC) at Maximum Quantity = USD$8,500 Now let ‘s draw two lines – one for Sales Revenue starting from 0 up to USD$15,000, and one for Total Costs (TC) starting from USD$3,500 up to USD$8,500. And Break-even Output can be seen on the x-axis at the point where Sales Revenue = Total Costs (TC) which is 175 chicken hamburgers. Answer: This hamburger restaurant must sell 175 chicken hamburgers per month in order to break-even. If it sells 174 chicken hamburgers, it will make a loss. If it sells 176 chicken hamburgers, it will make a profit. Costs and Revenues at the Break-even Point also need to be indicated on the chart. Sales Revenue (TC) at the Break-even Point = Price x Break-even Quantity Sales Revenue (TC) at the Break-even Point = USD$30 x 175 Sales Revenue (TC) at the Break-even Point = USD$5,250 Sales Revenue (TC) = Total Costs (TC) Total Costs (TC) = USD$5,250
Of course, calculating Break-even Point does not actually ensure the firm covers all its costs and makes profit. And of course, constructing the Break-even Chart does not mean that the firm has actually sold anything at all.
It is simply because Break-even Analysis is a decision-making tool based on theoretical Sales Revenue that managers hope to achieve and expected costs which may change any time.
 Articles: 1,400 · Readers: 740,000 · Views: 2,209,961
Articles: 1,400 · Readers: 740,000 · Views: 2,209,961 