Internal Rate of Return (IRR) shows the actual percentage rate of return from the investment with taking discounting into consideration.
Why is Internal Rate of Return (IRR) of a project important?
Internal Rate of Return (IRR) gives the rate of discount that yields Net Present Value (NPV) of zero considering the time value of money as it employs the discounting concept.
It uses discounted Cash Flows. Discounted Cash Flows are present values of future Cash Flows.
How to calculate Internal Rate of Return (IRR)?
Internal Rate of Return (IRR) is calculated by considering two Net Present Values (NPVs) with two different discount rates. One of the NPVs should be positive (NPV>0) and another one should be negative (NPV<0).
Internal Rate of Return (IRR) = RL + [NL / (NL – NH)] × (RH – RL)
where:
RH = Higher Interest Rate
RL = Lower Interest rate
NL = Net Present Value (NPV) at Lower Interest Rate
NH = Net Present Value (NPV) at Higher Interest Rate
Example of calculating Internal Rate of Return (IRR)
A business is thinking about purchasing a new machine at a cost of USD$35,000. The machine is going to be used for four years to produce products. The annual Net Cash Flows are showed below. What is the Internal Rate of Return (IRR) for this investment?
In Year 1, the Net Cash Flow is USD$15,000.
In Year 2, the Net Cash Flow is USD$15,000.
In Year 3, the Net Cash Flow is USD$10,000.
In Year 4, the Net Cash Flow is USD$10,000.
| Present Value of USD$1 | |||||||||||||
| Year: | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% | 12% | 14% | |
| 1 | 0.990 | 0.980 | 0.971 | 0.962 | 0.952 | 0.943 | 0.935 | 0.926 | 0.917 | 0.909 | 0.893 | 0.877 | |
| 2 | 0.980 | 0.961 | 0.943 | 0.925 | 0.907 | 0.890 | 0.873 | 0.857 | 0.842 | 0.826 | 0.797 | 0.769 | |
| 3 | 0.971 | 0.942 | 0.915 | 0.889 | 0.864 | 0.840 | 0.816 | 0.794 | 0.772 | 0.751 | 0.712 | 0.675 | |
| 4 | 0.961 | 0.924 | 0.888 | 0.855 | 0.823 | 0.792 | 0.763 | 0.735 | 0.708 | 0.683 | 0.636 | 0.592 | |
| 5 | 0.951 | 0.906 | 0.863 | 0.822 | 0.784 | 0.747 | 0.713 | 0.681 | 0.650 | 0.621 | 0.567 | 0.519 | |
| 6 | 0.942 | 0.888 | 0.837 | 0.790 | 0.746 | 0.705 | 0.666 | 0.630 | 0.596 | 0.564 | 0.507 | 0.456 | |
| 7 | 0.933 | 0.871 | 0.813 | 0.760 | 0.711 | 0.665 | 0.623 | 0.583 | 0.547 | 0.513 | 0.452 | 0.400 | |
| 8 | 0.923 | 0.853 | 0.789 | 0.731 | 0.677 | 0.627 | 0.582 | 0.540 | 0.502 | 0.467 | 0.404 | 0.351 | |
| 9 | 0.914 | 0.837 | 0.766 | 0.703 | 0.645 | 0.592 | 0.544 | 0.500 | 0.460 | 0.424 | 0.361 | 0.308 | |
| 10 | 0.905 | 0.820 | 0.744 | 0.676 | 0.614 | 0.558 | 0.508 | 0.463 | 0.422 | 0.386 | 0.322 | 0.270 | |
| 11 | 0.896 | 0.804 | 0.722 | 0.650 | 0.585 | 0.527 | 0.475 | 0.429 | 0.388 | 0.350 | 0.287 | 0.237 | |
| 12 | 0.887 | 0.788 | 0.701 | 0.625 | 0.557 | 0.497 | 0.444 | 0.397 | 0.356 | 0.319 | 0.257 | 0.208 | |
| 13 | 0.879 | 0.773 | 0.681 | 0.601 | 0.530 | 0.469 | 0.415 | 0.368 | 0.326 | 0.290 | 0.229 | 0.182 | |
| 14 | 0.870 | 0.758 | 0.661 | 0.577 | 0.505 | 0.442 | 0.388 | 0.340 | 0.299 | 0.263 | 0.205 | 0.160 | |
| 15 | 0.861 | 0.743 | 0.642 | 0.555 | 0.481 | 0.417 | 0.362 | 0.315 | 0.275 | 0.239 | 0.183 | 0.140 | |
| 16 | 0.853 | 0.728 | 0.623 | 0.534 | 0.458 | 0.394 | 0.339 | 0.292 | 0.252 | 0.218 | 0.163 | 0.123 | |
| 17 | 0.844 | 0.714 | 0.605 | 0.513 | 0.436 | 0.371 | 0.317 | 0.270 | 0.231 | 0.198 | 0.146 | 0.108 | |
| 18 | 0.836 | 0.700 | 0.587 | 0.494 | 0.416 | 0.350 | 0.296 | 0.250 | 0.212 | 0.180 | 0.130 | 0.095 | |
| 19 | 0.828 | 0.686 | 0.570 | 0.475 | 0.396 | 0.331 | 0.277 | 0.232 | 0.194 | 0.164 | 0.116 | 0.083 | |
| 20 | 0.820 | 0.673 | 0.554 | 0.456 | 0.377 | 0.312 | 0.258 | 0.215 | 0.178 | 0.149 | 0.104 | 0.073 |
The Net Cash Flows will then be discounted using the discount rate of 12% (RL=12%) and 20% (RH=20%) as the Net Present Value (NPV) equals zero somewhere in between these two discount rates.
Discount Rate = 12%:
In Year 1, the Discounted Net Cash Flow is USD$13,350.
In Year 2, the Discounted Net Cash Flow is USD$11,850
In Year 3, the Discounted Net Cash Flow is USD$7,100.
In Year 4, the Discounted Net Cash Flow is USD$6,400.
Now, sum up all the Discounted Net Cash Flows. The total Discounted Net Cash Flows equal to Net Present Value (NPV) being USD$3,700 (NL=USD$3,700).
Discount Rate = 20%:
In Year 1, the Discounted Net Cash Flow is USD$12,450.
In Year 2, the Discounted Net Cash Flow is USD$10,350
In Year 3, the Discounted Net Cash Flow is USD$5,800.
In Year 4, the Discounted Net Cash Flow is USD$4,800.
Now, sum up all the Discounted Net Cash Flows. The total Discounted Net Cash Flows equal to Net Present Value (NPV) being -USD$1,600 (NH = -USD$1,600).
RH = 20%
RL = 12%
NL = $3,700
NH = -$1,600
Internal Rate of Return (IRR) = RL + [NL / (NL – NH)] × (RH – RL)
Internal Rate of Return (IRR) = 12% + [$3,700 / ($3,700 – (-$1,600)] × (20% – 12%)
= 12% + [$3,700 / $5,300] × 8%
= 12% + 5.58%
= 17.58%
This Internal Rate of Return means that the actual percentage rate of return from the investment with taking discounting into consideration is 17.58%. The Internal Rate of Return (IRR) of 17.58% is when the Net Present Value (NPV) equals zero.
This percentage can be compared with Internal Rates of Return (IRR) of other projects or against the pre-set cut-off rate. For example, the firm will go ahead with all projects which yield more than 15%. Therefore, this investment is viable according to the cut-off criterion as it yields 17.58%.
Comment on the result of Internal Rate of Return (IRR)
As a general rule, when the discount rate increases, the Net Present Value (NPV) declines. And, when the discount rate decreases, the Net Present Value (NPV) grows.
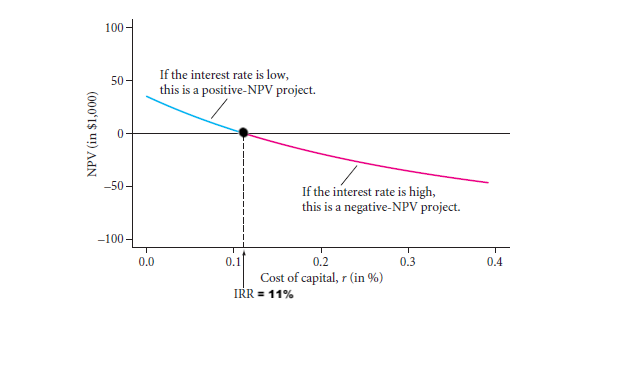
A. Choosing the most profitable project.
By comparing Internal Rate of Return (IRR) of many different projects, the most profitable investment can be chosen. The most profitable investment will have the highest Internal Rate of Return (IRR). Simply, the higher Internal Rate of Return (IRR), the more profitable the investment project is considering the time value of money. Simply, the lower Internal Rate of Return (IRR), the less profitable the investment project is considering the time value of money.
B. Choosing to invest in a project or not.
If the Internal Rate of Return (IRR) on an investment project is higher than the discount rate (the cost of borrowing capital), then the project will be pursued. It is because the Net Present Value (NPV) will be positive for any projects with the discount rate lower than the Internal Rate of Return (IRR). If the Internal Rate of Return (IRR) on an investment project is lower than the discount rate (the cost of borrowing capital), then the project will not be pursued. It is because the Net Present Value (NPV) will be negative for any projects with the discount rate higher than the Internal Rate of Return (IRR).
Briefly, if the Internal Rate of Return (IRR) of Project A is 16.50% and the Internal Rate of Return (IRR) of Project B is 5.20% while the cost of borrowing capital is 10%, the business should choose to invest in Project A instead of Project B.
Internal Rate of Return (IRR) – Evaluation
Internal Rate of Return (IRR) is a very popular method of evaluating investment projects comparing a percentage rate of return taking into consideration the time value of money. It should be considered together with Discounted Payback Period which considers project lengths and cash-flow timings while also taking into consideration the time value of money. And with Net Present Value (NPV) which considers the numerical value of investment projects while taking into consideration the time value of money.
Advantages of Internal Rate of Return (IRR) include:
- Allows to compare projects based on the real profitability. Managers can compare Internal Rate of Return (IRR) of a particular project with profitability of other alternative projects. By using a percentage rate of return adjusted for inflation, different projects costing different amounts in USD$ can be compared. Also, different projects can be put in rank order to choose the best investment project – with the highest Internal Rate of Return (IRR). Managers will always be looking for the highest percentage returns from their investments.
- Allows to compare the IRR with the cost of capital. Internal Rate of Return (IRR) is easily compared with the rate of interest. This percentage return of Internal Rate of Return (IRR) can be compared with the expected rate of interest over the life of the investment to make sure that the Net Present Value (NPV) remains positive.
- Allows to compare the IRR with the business’s criterion. Internal Rate of Return (IRR) can also be compared against the pre-set cut-off rate, or criterion of return, so the firm can only choose the most appropriate investments it prefers.
- Considers time value of money. Internal Rate of Return (IRR) does consider discounting. It brings to the present value the future Net Cash Flows. The timing of the Net Cash Flows and the size of them (their amounts) in arriving at the final appraisal are taken into consideration. Therefore, Value Internal Rate of Return (IRR) is helpful in evaluating investment projects as it compares project percentage returns from investment while taking the time value of money into account.
Disadvantages of Internal Rate of Return (IRR) include:
- Difficult to calculate and use. The calculation is very time consuming and tedious without using the Excel spreadsheet. Just take a look at the formula for calculating Internal Rate of Return (IRR) and what is needed to conduct this calculation.
- Not comprehensive enough to make final investment decisions. Internal Rate of Return (IRR) should only be regarded as one of the methods to assess competing investments. It could be used as a screening tool to include and eliminate certain projects based on their percentage rate of return adjusted for inflation, but it is inappropriate as a basis for making any sophisticated investment decisions. The results can only be compared with other projects based on profitability, but not based on cash returns adjusted for inflation. A large project worth USD$5,000,000 may have a higher Net Present Value (NPV) than a small project worth USD$500,000, but the latter may have much higher profitability on a percentage basis. Internal Rate of Return (IRR) does not give a monetary return, so it usually is not considered by itself.
In summary, remember that Investment Appraisal is evaluating the profitability or desirability of an investment project. There are two ways to do it. Quantitative Investment Appraisal is using techniques to study the financial issues of investment (think quantity in terms of percentages and money). And, Qualitative Appraisal which is studying non-financial issues that may impact an investment decision (think quality and impact).
